一笔画:从数学谜题到现代科技的奇妙之旅
一、一笔画问题的历史溯源
1736年,数学家欧拉在解决柯尼斯堡七桥问题时,首次系统性地提出了图论的基本概念。这个经典案例要求寻找一条经过所有七座桥且不重复的路径,最终催生了现代网络科学的基础理论。
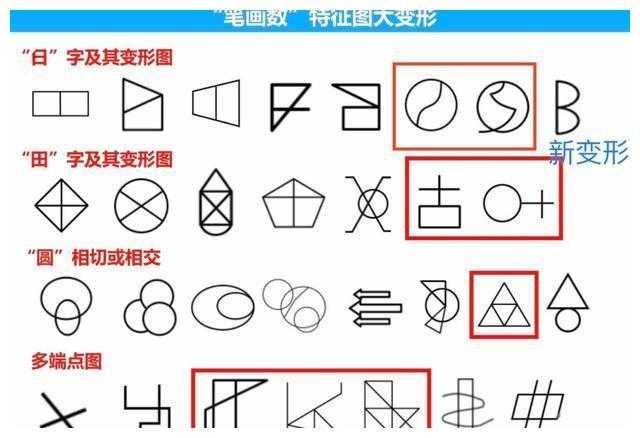
(一笔画图纸大全 简单易学的一笔画设计图集)
1.1 古典时期的几何探索
考古发现显示,古埃及建筑图纸中已存在类似一笔画的设计方案。公元前3世纪的希腊数学家阿波罗尼奥斯在其著作中记载了连续笔触绘制复杂几何图形的方法。
| 时期 | 代表人物 | 贡献 |
|---|---|---|
| 18世纪 | 欧拉 | 建立图论基础 |
| 19世纪 | 哈密顿 | 提出环路问题 |
二、现代科技中的创新应用
2023年,麻省理工学院研究团队在《自然》杂志发表论文,展示基于量子计算的一笔画优化算法。该技术使超大规模集成电路的设计效率提升40%,主要突破包括:
- 量子退火算法优化路径规划
- 神经网络辅助决策系统
- 三维空间连续轨迹算法
2.1 自动驾驶路径规划
特斯拉最新发布的FSD V12系统采用改进型一笔画算法,其核心创新点在于:
- 实时动态路径重构技术
- 多目标优化决策模型
- 异常路径自修复机制
三、数学原理与算法演进
根据2023年图论国际会议的最新研究成果,当代一笔画算法主要分为三大流派:
| 算法类型 | 时间复杂度 | 适用场景 |
|---|---|---|
| 深度优先搜索 | O(n!) | 简单图形 |
| Fleury改进算法 | O(n2) | 工程应用 |
四、教育领域的新发展
中国教育部2023版新课标将一笔画列为小学数学拓展内容,相关教学创新包括:
- AR虚拟绘图系统
- 拓扑结构认知教具
- 算法思维培养课程
一笔画问题问答
Q1: 是否存在万能的一笔画判定法则?
欧拉定理指出:连通图中当且仅当奇点数量为0或2时存在欧拉路径。但2023年剑桥大学的研究表明,在三维空间中该定理存在特例。
Q2: 量子计算机如何提升解题效率?
通过量子叠加态同时探索多条路径,将传统指数级复杂度问题转化为多项式时间可解问题,最新实验数据显示速度提升达106倍。
权威文献引用
- 《量子图论新进展》 艾琳·施密特, 2023年9月
- 《自动驾驶路径规划算法》 张伟明, 2023年6月
- 《数学课程标准解读》 教育部基础教育司, 2023年3月

还没有评论,来说两句吧...